|
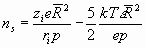 , (5) , (5)
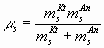 , (6) , (6)
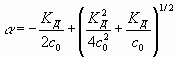 , (7) , (7)
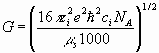 (8) (8)
где F – число Фарадея; е – заряд электрона; СV=5R/2 – теплоемкость; k – постоянная Больцмана; Т – температура, К; 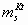 , , 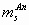 - массы сольватированных ионов, г; М – молекулярная масса растворителя, г; ns – сольватное число иона; - массы сольватированных ионов, г; М – молекулярная масса растворителя, г; ns – сольватное число иона; 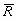 - эффективный радиус молекулы растворителя, см; ri и zi – радиус (см) и заряд иона; rs и rd – радиус сольватированного иона и дебаевский радиус экранирования; р – дипольный момент молекулы растворителя, ед.СГС; КД – константа диссоциации электролита; - эффективный радиус молекулы растворителя, см; ri и zi – радиус (см) и заряд иона; rs и rd – радиус сольватированного иона и дебаевский радиус экранирования; р – дипольный момент молекулы растворителя, ед.СГС; КД – константа диссоциации электролита; 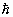 - постоянная Планка; NA – число Авогадро; - приведенная масса молекулы электролита, г; сi – молярная концентрация ионов (сi= c0); с0 – исходная молярная концентрация электролита. - постоянная Планка; NA – число Авогадро; - приведенная масса молекулы электролита, г; сi – молярная концентрация ионов (сi= c0); с0 – исходная молярная концентрация электролита. 3. Изоморфизм уравнений
При рассмотрении движения в поле вязких сил удобно ввести понятие подвижности b. Подвижность определяется как предельная скорость, приобретаемая телом под действием силы, равной единице, т. е.
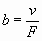
Таким образом, абсолютная подвижность в системе CGS равна скорости в сантиметрах в секунду, приобретаемой под действием силы в 1 дин. При рассмотрении движения ионов в качестве единицы силы обычно пользуются равным единице градиентом потенциала, действующим на ионный заряд.
Эквивалентная ионная электропроводность , связана простым соотношением с подвижностью. Из определения удельной электропроводности следует, что представляет собой ток, текущий через проводник с равным единице поперечным сечением под действием градиента потенциала, равного единице. Полный ионный заряд в единице объема равен Fc, если с измеряется в эквивалентах на единицу объема. Этот заряд, движущийся со скоростью b’, вызывает ток :
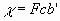 (9) (9)
или
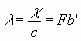 (10) (10)
Следовательно, для абсолютной подвижности имеем
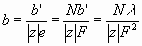 (11) (11)
Для макроскопической частицы, движущейся в идеальной гидродинамической среде, можно вычислить сопротивление трения. Оно выражается через размеры частицы и вязкость среды. Для сферической частицы Стоксом [8] выведена формула
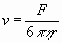 (12) (12)
где r - радиус сферы. Если ион движется по закону Стокса, его радиус определяется соотношением
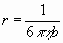 (13) (13)
Если b выражено через предельную эквивалентную электропроводность согласно уравнению (11), то получаем
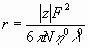 (14) (14)
Выразив r в 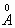 , а и в обычных единицах, придем к соотношению , а и в обычных единицах, придем к соотношению
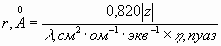 (14а) (14а)
Движение малых ионов не подчиняется закону Стокса, так как не выполняются необходимые предпосылки. Подвижность связана с коэффициентом диффузии D соотношением
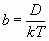 (15) (15)
где k—постоянная Больцмана. Это ведет к так называемой формуле Эйнштейна — Стокса:
Перейти на страницу: 1 2 3 4 5 6 7 8 |